前言

最近在尝试把FOC部署到STM32G030上，为了使FOC的运行更加丝滑，有必要在代码上进行一些优化以加快运算速度，因此，笔者参考了St电机库的源码，从中学习到了一些优化的技巧。

本文主要介绍FOC算法在St电机库中的实现方式，并与SimpleFOC进行简要对比。

数据定点化

众所周知，浮点数的运算相比整数运算要更耗费时间，在实际的电机控制应用中，一般会将算法中的数据变成定点数来处理（虽然SimpleFOC里面几乎全用的浮点数）。在谈论这个问题之前，我们先回顾一下浮点数和定点数在计算机中的存储方式。

浮点数

浮点数在内存中由三个部分组成：一个符号位、若干个指数位（表示小数点的位置），若干个尾数位。

定点数

定点数由于小数点的位置是固定的，因此不再需要指数位，一个定点数的小数点具体在哪个位置是由编写程序的人约定的

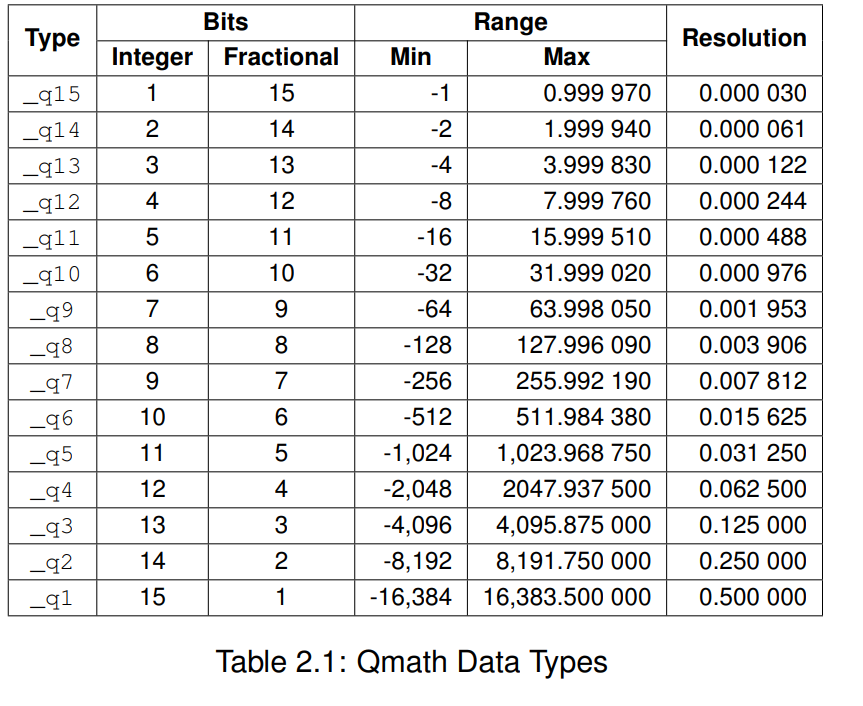
TI的IQMath库中对定点数类型的定义

SimpleFOC与St电机库数据处理的对比——以电流采样为例

float _readADCVoltageInline(const int pinA, const void* cs_params){
  uint32_t raw_adc = adcRead(pinA);
  return raw_adc * ((ESP32MCPWMCurrentSenseParams*)cs_params)->adc_voltage_conv;
}

可以看到SimpleFOC在电流计算的第一步就直接把原始值换算成了用浮点数表示的实际值。

  bSector = pHandle->_Super.Sector;
  hReg1 = *pHandle->pParams_str->ADCDataReg1[bSector] * 2;
  hReg2 = *pHandle->pParams_str->ADCDataReg2[bSector] * 2;

  switch ( bSector )
  {
    case SECTOR_4:
    case SECTOR_5:
      /* Current on Phase C is not accessible     */
      /* Ia = PhaseAOffset - ADC converted value) */
      wAux = ( int32_t )( pHandle->PhaseAOffset ) - ( int32_t )( hReg1 );
      /* Saturation of Ia */
      if ( wAux < -INT16_MAX )
      {
        pStator_Currents->a = -INT16_MAX;
      }
      else  if ( wAux > INT16_MAX )
      {
        pStator_Currents->a = INT16_MAX;
      }
      else
      {
        pStator_Currents->a = ( int16_t )wAux;
      }

以上是三电阻电流采样函数的一部分，由于采用三电阻，因此要依电压扇区决定舍弃哪一相的电流值。主要做的事情是把原始值拿出来乘了个二然后限制了一下范围，乍一看有点摸不着头脑。

根据初始化代码指定的ADC转换模式找到了对应的数据对齐方式图，可以发现乘二的操作其实就是把12位的原始值映射到了16位上（因为St电机库用的是q15的定点数）。

定点数的运算

定点数运算-维基百科

定点数的加减法比较简单，直接按一般方法加减即可。在乘除运算时会遇到一些问题。比如两个q15的定点数相乘，要想保留全部的精度，结果应该是一个q30的数，如果想要得到一个与原来长度相同的定点数，就要舍弃一些精度来对结果进行裁剪，比如在本例中，要想让结果变成q15，需要把q30的结果右移15位。除法的规则类似。

以下是St电机库中Clarke变换中定点数运算的例子：

  int32_t a_divSQRT3_tmp, b_divSQRT3_tmp ;
  int32_t wbeta_tmp;
  int16_t hbeta_tmp;

  Output.alpha = Input.a;
  a_divSQRT3_tmp = divSQRT_3 * ( int32_t )Input.a;
  b_divSQRT3_tmp = divSQRT_3 * ( int32_t )Input.b;
  wbeta_tmp = ( -( a_divSQRT3_tmp ) - ( b_divSQRT3_tmp ) -
                 ( b_divSQRT3_tmp ) ) >> 15;

扇区判断

在没有加入电流环时，我们无法对U轴和D轴的电流进行精确的控制，输出电压的D分量一般设为0，此时电压矢量的扇区可以直接由转子机械角度换算得到，但在加入电流环之后，D分量不一定为零，因此需要针对输出电压矢量重新判断扇区。

SimpleFOC的方案

SimpleFOC新版本加入了电流环的功能，因此它里面也有这部分的代码。它对电压矢量扇区判断的操作非常直球，既然加入D分量会使得电角度相对转子角度发生偏移，那我把这个偏移的角度加上去再判断不就完事了吗，于是就有了下面的代码：

if(Ud){ // only if Ud and Uq set
        // _sqrt is an approx of sqrt (3-4% error)
        Uout = _sqrt(Ud*Ud + Uq*Uq) / driver->voltage_limit;
        // angle normalisation in between 0 and 2pi
        // only necessary if using _sin and _cos - approximation functions
        angle_el = _normalizeAngle(angle_el + atan2(Uq, Ud));
      }else{// only Uq available - no need for atan2 and sqrt
        Uout = Uq / driver->voltage_limit;
        // angle normalisation in between 0 and 2pi
        // only necessary if using _sin and _cos - approximation functions
        angle_el = _normalizeAngle(angle_el + _PI_2);
      }

可以看到它计算这个偏移角度是通过atan2函数实现的，在效率上还是会打点折扣，那么有没有优雅一点的方法呢？

St电机库的方案

(其实这个方案不止St在用，大部分正经FOC的扇区判断基本上都是这样算的)

首先将PI控制器输出的两个分量进行反Park变换得到α和β分量，然后通过以下三个式子各自的正负就能判断扇区：

为什么用这仨玩意儿就能判断出扇区呢，我们把这几个式子稍微变一下形就很直观了。

已知：

那上面的式子就可以如下表达：

是不是就一目了然了，X划分的是上半和下半的扇区，Y划分的是左上和右下的扇区，Z划分的是右上和左下的扇区，确定了这三个量，扇区自然就能确定了。对照一下St的源码：

 wUAlpha = Valfa_beta.alpha * ( int32_t )pHandle->hT_Sqrt3;
 wUBeta = -( Valfa_beta.beta * ( int32_t )( pHandle->PWMperiod ) ) * 2;

  wX = wUBeta;
  wY = ( wUBeta + wUAlpha ) / 2;
  wZ = ( wUBeta - wUAlpha ) / 2;

这里只是进行了一些等比例的缩放，方便后续使用，道理是一样的。

这三个量不仅用于判断扇区，还可以直接用于输出占空比的计算，首先回顾一下一个周期内两个矢量持续时间的计算公式（以扇区I为例）：

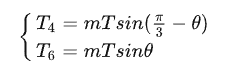
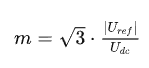
是不是看起来有点眼熟，其实就是上面那三个玩意儿凑的，其它扇区也是同理。

下面是St电机库计算占空比的部分代码：

if ( wY < 0 )
  {
    if ( wZ < 0 )
    {
      pHandle->Sector = SECTOR_5;
      wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wY - wZ ) / ( int32_t )262144 );
      wTimePhB = wTimePhA + wZ / 131072;
      wTimePhC = wTimePhA - wY / 131072;
      pHandle->lowDuty = wTimePhC;
      pHandle->midDuty = wTimePhA;
      pHandle->highDuty = wTimePhB;
    }

可以看到最终输出占空比可以由这三个量计算得到，至于底下除的那个131072，我也不是很明白是怎么来的，但这只是对数据进行了一些缩放来匹配定时器，基本思路是很清楚的。

磁链圆限制

关于输出电压矢量最大是√3/2Udc这码事

不少人应该都看过这个图，图中这个六边形是输出的最大电压范围，这是由于一个周期内Tx和Ty之和是不可能大于T的，它的内切圆是能让转矩稳定输出的最大电压范围，当电压矢量超出这个圆时，某些位置的电压超出了六边形，逆变器输出不了，就会造成电机的转矩不稳定，这一现象也被称为过调制。

将Tx+Ty<=T这个条件代入SVPWM的公式中是可以求出Uref的范围的：

√3/2Udc就是这个内切圆的半径。

在实际的应用中，考虑到管子的开关时间和电流采样等因素，这个圆还要再小一点。但PI控制器输出的电压矢量是有可能超出这个圆的，遇到这种情况时，就需要对矢量进行缩小，将其限制在圆的范围内。

缩小电压矢量的方法

要把电压矢量缩到圆内，只需要将q和d分量缩小一定倍数即可，设q和d分量的缩小系数为k，有：

式中出现的根号运算也比较费时，因此St使用查表的方式来求取这个系数。

__weak qd_t Circle_Limitation( CircleLimitation_Handle_t * pHandle, qd_t Vqd )
{
  uint16_t table_element;
  uint32_t uw_temp;
  int32_t  sw_temp;
  qd_t local_vqd = Vqd;

  sw_temp = ( int32_t )( Vqd.q ) * Vqd.q +
            ( int32_t )( Vqd.d ) * Vqd.d;

  uw_temp = ( uint32_t ) sw_temp;

  /* uw_temp min value 0, max value 32767*32767 */
  if ( uw_temp > ( uint32_t )( pHandle->MaxModule ) * pHandle->MaxModule )
  {

    uw_temp /= ( uint32_t )( 16777216 );

    /* wtemp min value pHandle->Start_index, max value 127 */
    uw_temp -= pHandle->Start_index;

    /* uw_temp min value 0, max value 127 - pHandle->Start_index */
    table_element = pHandle->Circle_limit_table[( uint8_t )uw_temp];

    sw_temp = Vqd.q * ( int32_t )table_element;
    local_vqd.q = ( int16_t )( sw_temp / 32768 );

    sw_temp = Vqd.d * ( int32_t )( table_element );
    local_vqd.d = ( int16_t )( sw_temp / 32768 );
  }

  return ( local_vqd );
}

参考文章

ST电机库v5.4.4源代码分析(3): α、β方向的电流值与三相PWM 波形的联系
FOC中的SVPWM原理细讲

最后修改：2023 年 08 月 20 日
© 允许规范转载
V我五十